The accurate detection of object boundaries via active contours is an ongoing research topic in computer vision. Most active contours converge towards some desired contour by minimizing a sum of internal (prior) and external (image measurement) energy terms. Such an approach is elegant, but suffers from a slow convergence rate and frequently mis-converges in the presence of noise or complex contours. To address these limitations, a decoupled active contour (DAC) is developed which applies the two energy terms separately. Essentially, the DAC consists of a measurement update step, employing a Hidden Markov Model (HMM) and Viterbi search, and then a separate prior step, which modifies the updated curve based on the relative strengths of the measurement uncertainty and the non-stationary prior. By separating the measurement and prior steps, the algorithm is less likely to mis-converge; furthermore, the use of a Viterbi optimizer allows the method to converge far more rapidly than energy-based iterative solvers. The results clearly demonstrate that the proposed approach is robust to noise, can capture regions of very high curvature, and exhibits limited dependence on contour initialization or parameter settings. Compared to five other published methods and across many image sets, the DAC is found to be faster with better or comparable segmentation accuracy.
Finding the visual boundary using the Viterbi search
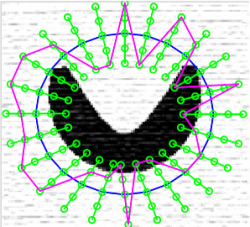
The “visual boundary estimation” problem is formulated as a shortest path finding puzzle on a discrete trellis. Viterbi search algorithm is employed to find the shortest path.
Circular trellis with an initial snake (blue circle), one possible, albeit unlikely snake (magenta), normals (green lines) and nodes (small circles along the normals)
Generation of non-stationary prior via importance sampling
To capture high curvature more samples are placed near high curvature to lower the penalty on curvature. The curvature guided importance sampling method is demonstrated below:

Statistical data fusion
The non-stationary prior is fused with measured boundary using a Linear Baysian estimation formulation. The effect measurement uncertainties is demonstrated below:

